[Algorithm] 시간복잡도 Big-O notation

시간복잡도 Time Complexity

시간복잡도는 알고리즘이 얼마나 빠른지 측정하는 방법이다.
알고리즘이 동작하는 환경(하드웨어 조건)이 모두 다르기때문에 단순히 시간으로 측정하는 것이 아니고
얼마나 많은 단계를 거쳐 동작하는가를 중심으로 속도를 판단한다.

Big-O notation

어떤 알고리즘이 얼마나 느린지, 빠른지 설명하기 위해 Big-O 표기법을 활용한다.
이 알고리즘은 n개의 요소가 있을때 n만큼의 단계가 필요하다 라고 설명하기보다
그 알고리즘은 O(n)의 시간복잡도를 가지고 있다 라고 표현하는 것이다.

시간복잡도를 비교할 수 있는 여러가지 Big-O 표기가 있는데
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!) 의 순서로 볼 수 있다.

O(1) : Constant time

O(1)은 아무리 요소가 많은 자료가 오더라도 한번의 실행으로 절차가 끝나는 알고리즘을 말한다.

function solution(arr) {
  console.log(arr[0]);
}

Big-O는 함수의 디테일에는 관심이 없다.
따라서 200개의 요소를 출력하는 함수라해도, 표현은 O(1)으로 하면된다.

O(n) : Linear time

O(n)은 요소의 수만큼 절차가 실행되는 알고리즘을 말한다.
인풋이 커지는만큼 절차가 늘어난다.

function solution(arr) {
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
}

O(log n)

O(log n)은 로그 시간복잡도를 지니며, 인풋이 큰 경우에도 절차를 확 줄일 수 있다.

function solution(arr) {
  for (let i = 1; i <= n; i *= 2) {
    console.log(i);
  }
}

O(n log n)

O(n)의 절차 내부에서 O(log n)가 실행되는 것을 말한다.

function solution(arr) {
  for (let i = 0; i < n; i++) {
    for (let j = 1; j <= n; j *= 2) {
      // ...
    }
  }
}

O(n²)

O(n) 내부에서 O(n)이 실행되는 것을 말한다.

function solution(arr) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      // ...
    }
  }
}

이 외에 O(2ⁿ) 와 O(n!)의 시간복잡도는
코딩테스트에서 사용할 일이 없고 사용해서도 안된다.

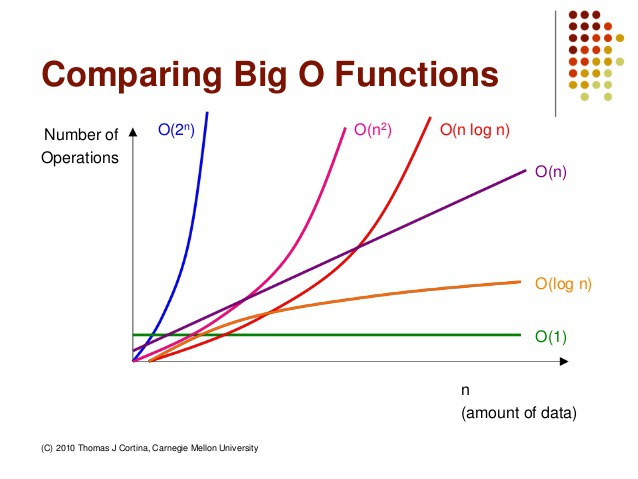시간복잡도 그래프